1. Accueil
  2. Références
  3. ► B.O.E.N.
  4. ► Terminale

► Terminale

Baccalauréat TERMINALE
Programme B.O.E.N. 2009
validité 2019 - 2020 et 2020 - 2021
→ Capacités Bac Terminale 2009 - 2021Cliquez ici !

 S 1.1. Statistiques à 2 variables
(Groupement A, B et C) 
Représenter à l’aide des TIC un nuage de points.
Déterminer le point moyen.
Déterminer, à l’aide des TIC, une équation de droite qui exprime de façon approchée une relation entre les ordonnées et les abscisses des points du nuage.
Utiliser cette équation  pour interpoler ou  extrapoler. 
S 1.2. Probabilités
(Groupement A, B et C)
Passer du langage probabiliste au langage courant et réciproquement.
Calculer la probabilité d’un événement par addition des probabilités d’événements élémentaires.
Reconnaître et réinvestir des situations de probabilités issues d’expériences aléatoires connues : tirages aléatoires avec ou sans remise, urnes.
Calculer la probabilité d’un événement contraire 
Calculer la probabilité de la réunion  d’événements  incompatibles.
Utiliser la formule reliant la probabilité de 
A 2.1. Suites numériques 2
(Groupement A, B et C) 
Appliquer les formules donnant le terme de rang n en fonction du premier terme et de la raison de la suite. 
A 2.2. Fonctions dérivées et étude des variations d’une fonction
(Groupement A, B et C)
Utiliser les formules et les règles de dérivation pour déterminer la dérivée d’une fonction.
Étudier, sur un intervalle donné, les variations d’une fonction à partir du calcul et de l’étude du signe de sa dérivée.  
Commentaires: Étant donnée une fonction f dérivable sur un intervalle I, la fonction qui à tout nombre x de I associe le nombre dérivé de la fonction f  en x est appelée fonction dérivée de la fonction f sur I et est notée f ’. Dans les énoncés de problèmes ou d’exercices, les formules, admises, sont à choisir dans un formulaire spécifique donné en annexe.  Appliquer ces formules à des exemples ne nécessitant aucune virtuosité de calcul.Les formules sont progressivement mises en œuvre pour déterminer les dérivées de fonctions polynômes de degré inférieur ou égal à 3. 
Dresser son tableau de variation.
Commentaires: Étant donnée une fonction f dérivable sur un intervalle I, la fonction qui à tout nombre x de I associe le nombre dérivé de la fonction f  en x est appelée fonction dérivée de la fonction f sur I et est notée f ’. Dans les énoncés de problèmes ou d’exercices, les formules, admises, sont à choisir dans un formulaire spécifique donné en annexe.  Appliquer ces formules à des exemples ne nécessitant aucune virtuosité de calcul.Les formules sont progressivement mises en œuvre pour déterminer les dérivées de fonctions polynômes de degré inférieur ou égal à 3. 
Déterminer un extremum d’une fonction sur un intervalle donné à partir de son sens de variation.
Commentaires: Les théorèmes liant le sens de variation d’une fonction et le signe de sa dérivée sont admis.Le tableau de variation est un outil d’analyse, de réflexion voire de preuve. Constater, à l’aide de la fonction cube, que le seul fait que sa dérivée s’annule ne suffit pas pour conclure qu’une fonction possède un extremum.
A 2.4. Fonctions logarithme et exponentielles
(Groupement  A et B)
Étudier les variations et représenter graphiquement la fonction logarithme népérien, sur un intervalle donné.
Étudier les variations et représenter graphiquement la fonction logarithme décimal, sur un intervalle donné.
Exploiter une droite tracée sur du papier semi- logarithmique.
Capacité du groupement C mais pas des groupements A ou  B enspécialité BAC domaine  BTP
Étudier les variations et représenter graphiquement la fonction x a ex sur un intervalle donné.
Interpréter eb comme la  solution de  l’équation ln (x) = b.
Étudier les variations et représenter graphiquement la fonction x ? ex sur un intervalle donné.
Étudier les variations des fonctions x ? eax a (a réel non nul).
Résoudre des équations du type eax = b et des inéquations du type eax  ≥ b (ou eax  ≤ b)
Résoudre des équations du type ln (ax) = b (avec a > 0) et des inéquations du type ln (ax) ≥ b (ou ln (ax) ≤ b) (avec a > 0).
G 3.1. Géométrie dans le plan et dans l’espace : consolidation
(Groupement B)
Représenter, avec ou sans TIC, la section d’un solide usuel par un plan.
Représenter, avec ou sans TIC, la section d’un solide usuel par un plan.
Identifier un solide usuel dans un objet donné, à partir d’une représentation géométrique de ce dernier.
Lire et interpréter une représentation d’un solide.
Isoler une figure plane extraite d’un solide à partir d’une représentation.
Utiliser les définitions, propriétés et théorèmes mis en place dans les classes précédentes pour identifier, représenter et étudier les figures planes et les solides cités dans ce paragraphe.
G 3.2. Vecteurs 2 (Groupement B)
Calculer la norme d’un vecteur dans un repère orthonormal dans l’espace.
Cette capacité est en séquence "Trigonométrie 2"
G 3.2. Trigonométrie 2 (Groupement A)
Établir des liens entre le vecteur de Fresnel d'une tension ou d'une intensité sinusoïdale de la forme a.sin(ωt + φ) et la courbe représentative de la fonction qui à t associe a.sin(ωt + φ),
Mettre en œuvre les formules exprimant cos(a+b) et sin(a+b) en fonction de cosa, sina, cosb, sinb,
Résoudre les équations de la forme cos(x) = a, sin(x) = b et sin(ωt+φ ) = c,
Estimer, à l'aide d'un tableur grapheur ou d'une calculatrice, la (les) solution(s) dans un intervalle donné de l'équation f(x)=λ avec λ réel donné et f(x)= cos(x) ou f(x)= sin(x) et de l'équation sin(ωt+φ ) = c,
PROGRAMME COMPLEMENTAIRE PREPARATOIRE AU SECTIONS DE TECHNICIEN SUPERIEUR (BTS)
Produit Scalaire (Gpt A et B)
Utiliser les trois expressions du produit scalaire de deux vecteurs pour déterminer des longueurs et des angles.
Connaissances : Définition du produit scalaire de deux vecteurs.
Commentaires: Les trois expressions du produit scalaire de deux vecteurs sont les suivantes :
si, dans un repère orthonormal, les vecteurs 


Connaissances : Formules exprimant sin (a + b) et cos (a + b) en fonction de cos a, cos b, sin a, sin b.
Commentaires:  Deux des trois expressions du produit scalaire de deux vecteurs sont utilisées pour élaborer la formule donnant cos (a - b).

Connaissances : Propriétés du produit scalaire de deux vecteurs :
Commentaires: Ces propriétés sont admises.
 

Utiliser les trois expressions du produit scalaire de deux vecteurs pour déterminer des longueurs et des angles.
Connaissances : Définition du produit scalaire de deux vecteurs.
Commentaires: Les trois expressions du produit scalaire de deux vecteurs sont les suivantes :
Les trois expressions du produit scalaire de  deux vecteurs sont les suivantes :

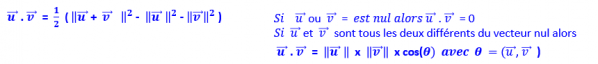
Capture produit scalaire
ur vr = ur + vr - ur - v
si ur ou vr est nul alors ur . vr = 0.
si ur et vr sont tous les deux différents du
vecteur nul alors ur . vr = u? ´ v? ´ cosq, avec q  = ( ur , vr ).
si, dans un repère orthonormal, les vecteurs ur et vr ont pour coordonnées respectives (x , y) et (x' , y’) alors ur . vr = xx’ + yy’
si, dans un repère orthonormal, les vecteurs 
Connaissances : Formules exprimant sin (a + b) et cos (a + b) en fonction de cos a, cos b, sin a, sin b.
Commentaires:  Deux des trois expressions du produit scalaire de deux vecteurs sont utilisées pour élaborer la formule donnant cos (a - b).
Connaissances : Propriétés du produit scalaire de deux vecteurs :
Commentaires: Ces propriétés sont admises.
Nombres complexes (Gpt A et B)
Représenter, dans le plan complexe, la somme de deux nombres complexes et le produit d’un nombre complexe par un réel. Connaissances : Somme, produit, quotient de deux nombres complexes.
Effectuer des calculs dans l’ensemble C des nombres complexes ; donner le résultat sous forme algébrique.
Écrire un nombre complexe sous forme trigonométrique.
Connaissances : Module et arguments d’un nombre complexe non nul.
Passer de la forme algébrique d’un nombre complexe à sa forme trigonométrique et réciproquement.
Calcul intégral (Gpt A et B)
Savoir que si F est une primitive d’une fonction f sur un intervalle, F + k (où k est une constante) est aussi une primitive de f.
Connaissances : Primitives d’une fonction sur un intervalle.
Commentaires: Conjecturer cette propriété en déterminant, par expérimentation, parmi plusieurs fonctions données, celles dont les fonctions dérivées sont égales.
Utiliser un tableau donnant les primitives des fonctions usuelles suivantes :  x ?k  ,  x?x ,  x ?x² , x ?x3 , x ?xn  et x ? ?1/x
Connaissances : Primitives d’une somme de fonctions, du produit d’une fonction par un réel.
Commentaires:  Entraîner les élèves à retrouver ces primitives par lecture inverse des formules de dérivation. Dans tous les autres cas, une primitive est donnée.
Déterminer, avec ou sans TIC, les primitives d’une somme de fonctions, du produit d’une fonction par un réel.
Interpréter, dans le cas d’une fonction positive, une intégrale comme l’aire d’une surface.
Primitives (Gpt C)
Savoir que si F est une primitive d’une fonction f sur un intervalle, F + k (où k est une constante) est aussi une primitive de f.
Connaissances : Primitives d’une fonction sur un intervalle.
Commentaires: Conjecturer cette propriété en déterminant, par expérimentation, parmi plusieurs fonctions données, celles dont les fonctions dérivées sont égales.
Utiliser un tableau donnant les primitives des fonctions usuelles suivantes :  x ?k  ,  x?x ,  x ?x² , x ?x3 , x ?xn  et x ? ?1/x
Connaissances : Primitives d’une somme de fonctions, du produit d’une fonction par un réel.
Commentaires:  Entraîner les élèves à retrouver ces primitives par lecture inverse des formules de dérivation. Dans tous les autres cas, une primitive est donnée.
Déterminer, avec ou sans TIC, les primitives d’une somme de fonctions, du produit d’une fonction par un réel.
Fonctions logarithme et exponentielle de base e (Gpt C)
Étudier les variations et représenter graphiquement la fonction logarithme népérien, sur un intervalle donné.
Connaissances : Fonction logarithme népérien x ->  ln x. Définition du nombre e. Propriétés opératoires de la fonction logarithme népérien.
Commentaires:  La fonction ln est la fonction définie pour x > 0, qui s’annule en 1 et dont la dérivée est la fonction inverse. L’étude des variations est conduite à l’aide de la dérivée. Ces propriétés sont conjecturées à l’aide de la courbe représentative de la fonction logarithme népérien ou à l’aide de la calculatrice. Toute virtuosité dans l’utilisation de ces propriétés est exclue.
Interpréter eb comme la  solution de  l’équation ln x = b. Connaissances : La fonction exponentielle x ->  ex
Étudier les variations et représenter graphiquement la fonction x ? ex sur un intervalle donné.  
Connaissances : Propriétés opératoires de la fonction exponentielle de base e.
Commentaires: Conjecturer, à l’aide de la calculatrice, que ln (eb) = b. L’unicité de la solution est montrée à l’aide de la courbe représentative de la fonction logarithme népérien. La représentation graphique de la fonction x ->  ex est obtenue à l’aide des TIC. Ces propriétés sont conjecturées à l’aide de la courbe représentative de la fonction logarithme népérien ou à l’aide de la calculatrice.
Étudier les variations des fonctions x ? eax a (a réel non nul). 
Connaissances : Dérivée des fonctions x ->  eax (a réel non nul).
Commentaires: Illustrer le cas a = 1 à l’aide des coefficients directeurs de quelques tangentes. Dans les énoncés de problèmes ou d’exercices, la formule, admise, est à choisir dans un formulaire spécifique donné en annexe.  Les fonctions  x  -> qx (avec q =10 et q = 1/2) sont étudiées selon les besoins du domaine professionnel ou des autres disciplines. 
Résoudre des équations du type eax = b et des inéquations du type eax > = b (ou eax > = b)
Connaissances : Pocessus de résolution
:Pocessus de résolution
Connaissances des équations du type ln (ax) = b (avec a > 0) et des inéquations du type ln (ax) > = b (ou ln (ax) =< b) (avec a > 0). Résoudre
Baccalauréat
Classe de TERMINALE
BOEN 2019 applicable septembre 2021

Statistique et probabilités
Algèbre – Analyse
Géométrie
Algorithmique et programmation
(groupements A, B et C)
Automatismes
(groupements A, B et C)
Vocabulaire ensembliste et logique
(groupements A, B et C)
Programme complémentaire en vue
de la préparation à une poursuite d’études

Mathématiques

Référentiel Mathématiques
→ Spe003 annexe2 1239843 Spe003 annexe2 1239843 (535.97 Ko)

Nouveaux programmes
MATHEMATIQUES
source: Académie Clermont-Ferrand
Visio 08/04/201 - Service d'Inspection
Inspection du second degré
Claire MARLIAS, IEN EG mathématiques-physique –chimie
→ Presentation nouveaux programmes mathsPrésentation Nouveaux Programmes M (605.21 Ko)

Grille nationale d'Evaluation
Mathématiques - Physique - Chimie
→ Grillenationaleevaluationmaths sciences2013 251959 Grille Nationale D'Evaluation (223.44 Ko)

Liste des groupements
Mathématiques - Physique - Chimie
→  Liste groupements bac pro 614266 1Liste groupements BAC PRO (21.71 Ko)


 

 

Physique - Chimie

Référentiel Physique - Chimie
→Spe004 annexe2 1239694 Spe004 annexe2 1239694 (574.99 Ko)

Nouveaux programmes
PHYSIQUE - CHIMIE
Source: Académie Clermont-Ferrand
Visio 08/04/201 - Service d'Inspection
Inspection du second degré
Claire MARLIAS, IEN EG mathématiques-physique –chimie
→ Presentation nouveaux programmes pcPrésentation Nouveaux Programmes PC (1.42 Mo)

Grille nationale d'Evaluation
Mathématiques - Physique - Chimie
→ Grillenationaleevaluationmaths sciences2013 251959 Grille Nationale D'Evaluation (223.44 Ko)

Liste des groupements
Mathématiques - Physique - Chimie
→  Liste groupements bac pro 614266 1Liste groupements BAC PRO (21.71 Ko)

L’enseignement de mathématiques et de physique-chimie en classes de première et terminale de la voie professionnelle concourt à la formation intellectuelle, professionnelle et civique des élèves1.

Il les prépare au baccalauréat professionnel dans l’objectif d’une insertion professionnelle ou d’une poursuite d’études supérieures réussies.
Le programme est conçu à partir des intentions suivantes :

 - Permettre à tous les élèves d’élargir leurs acquis dans les domaines des mathématiques et de la physique-chimie, afin de consolider leurs connaissances et leurs compétences dans ces domaines, dans une perspective d’évolution professionnelle et de formation personnelle ;

 - Approfondir la formation des élèves aux activités de nature mathématique, physique et chimique en poursuivant la pratique des démarches mathématique et expérimentale ;

 -  Fournir aux élèves des outils mathématiques et scientifiques utiles aux enseignements généraux et professionnels ;

 -  Assurer les bases mathématiques et scientifiques indispensables à la formation tout au long de la vie et à une éventuelle poursuite d’études ;

 - Participer au développement de compétences transversales qui contribuent à l’insertion sociale et professionnelle des élèves en leur permettant de devenir des citoyens éclairés et des professionnels capables de s’adapter à l’évolution des métiers liée entre autres à la transformation digitale et à la prise en compte des contraintes énergétiques et environnementales.

1 Ici, comme dans l’ensemble du texte, le terme « élève » désigne l’ensemble des publics de la voie professionnelle : élève sous statut scolaire, apprenti ou adulte en formation.

Dans le prolongement des enseignements dispensés précédemment, cinq compétences communes aux mathématiques et à la physique-chimie sont travaillées.
Elles permettent de structurer la formation et l’évaluation des élèves.

L’ordre de leur présentation ne prescrit pas celui dans lequel ces compétences seront mobilisées par l’élève dans le cadre d’activités.

Une liste non limitative de capacités associées à chacune des compétences indique la façon dont ces dernières peuvent être mises en oeuvre.
Leur niveau de maîtrise dépend de l’autonomie et de l’initiative requises dans les activités proposées aux élèves.

Ces compétences sont plus ou moins mobilisées selon les activités et il convient de diversifier les situations afin de les développer toutes.

Grille nationale d'évaluation
BAC PRO
Mathématiques Physique Chimie
→ Grille nationale d'évaluation BAC MPC  (212.57 Ko)

Compétences et capacités associées
S’approprier
 - Rechercher, extraire et organiser l’information.
 - Traduire des informations, des codages.
Analyser - Raisonner
 - Émettre des conjectures, formuler des hypothèses.
 - Proposer une méthode de résolution.
 - Choisir un modèle ou des lois pertinentes.
 - Élaborer un algorithme.
 - Choisir, élaborer un protocole.
 - Évaluer des ordres de grandeur.
Réaliser
 - Mettre en oeuvre les étapes d’une démarche.
 - Utiliser un modèle.
 - Représenter (tableau, graphique...), changer de registre.
 - Calculer (calcul littéral, calcul algébrique, calcul numérique exact ou approché, instrumenté ou à la main).
 - Mettre en oeuvre un algorithme.
 - Expérimenter – en particulier à l’aide d’outils numériques (logiciels ou dispositifs d’acquisition de données…).
 - Faire une simulation.
 - Effectuer des procédures courantes (représentations, collectes de données, utilisation du matériel…).
 - Mettre en oeuvre un protocole expérimental en respectant les règles de sécurité à partir d’un schéma ou d’un descriptif.
 - Organiser son poste de travail.
Valider
 - Exploiter et interpréter les résultats obtenus ou les observations effectuées afin de répondre à une problématique.
 - Valider ou invalider un modèle, une hypothèse en argumentant.
 - Contrôler la vraisemblance d’une conjecture.
 - Critiquer un résultat (signe, ordre de grandeur, identification des sources d’erreur), argumenter.
 - Conduire un raisonnement logique et suivre des règles établies pour parvenir à une conclusion (démontrer, prouver).
Communiquer
À l’écrit comme à l’oral :
- rendre compte d’un résultat en utilisant un vocabulaire adapté et choisir des modes de représentation appropriés ;
- expliquer une démarche.

 1.1 - Statistiques à 2 variables
À l’aide d’outils numériques :
- Choisir un modèle adapté pour réaliser un ajustement d’un nuage de points associé à une série statistique à deux variables ;
- Utiliser un ajustement pour interpoler ou extrapoler des valeurs inconnues.
Ajustement d’un nuage de points associé à une série statistique à deux variables quantitatives.
Commentaires : Les ajustements réalisés ne sont pas uniquement affines. Aucune justification théorique du modèle choisi n’est attendue. On indique aux élèves l’ajustement à réaliser (ajustement de x en y ou de y en x).

1.2 - Probabilités
Représenter par un arbre de probabilités pondéré une situation aléatoire donnée.
Arbres de probabilités pondérés : noeud, branche, chemin.
Exploiter la lecture d’un arbre de probabilités pondéré pour déterminer les probabilités des événements associés aux différents chemins. Dans des cas simples, calculer une probabilité à l’aide de la formule des probabilités totales.
Probabilité conditionnée par un événement de probabilité non nulle. Règles de calculs des probabilités. Formule des probabilités totales.
Montrer que deux événements sont indépendants.
Indépendance de deux événements de probabilités non nulles. Dans le cas d’événements indépendants : P(A?B) = P(A) × P(B)
Commentaires:
- Les premiers arbres pondérés et le vocabulaire associé sont introduits à partir des tableaux croisés d’effectifs vus en classe de première ; leur utilisation est ensuite généralisée aux cas d’expériences aléatoires à plusieurs épreuves, indépendantes ou non.
- La formule des probabilités totales est systématiquement mise en relation avec un arbre de probabilités pondéré et appliquée sans formalisme. Elle est présentée sur un exemple et peut illustrer, dans des situations simples, un raisonnement par disjonction de cas.

2.1 - Suites numériques 2
Calculer un terme de rang donné d’une suite géométrique définie par son premier terme et par une relation de récurrence ou par l’expression du terme de rang n.
Réaliser et exploiter une représentation graphique du nuage de points (n ; un) dans le cas où (un) est une suite géométrique.
Déterminer le sens de variation d’une suite géométrique à l’aide de sa raison q avec q > 0 et de son premier terme.
Suites géométriques de raison strictement positive : définies par la relation un+1 = un × q et la donnée du premier terme ; expression du terme de rang n en fonction du premier terme et de la raison ; sens de variation.
Calculer la somme des n premiers termes d’une suite géométrique avec ou sans outils numériques.
Somme des n premiers termes d’une suite géométrique.

Exemples d’algorithmes ou d’activités numériques
- Calculer un terme de rang donné d’une suite géométrique.
- Calculer la somme d’un nombre fini de termes d’une suite numérique.
- Générer une liste de termes d’une suite géométrique et les représenter par un nuage de points de coordonnées (

2.2 - Fonctions polynômes de degré 3
Étudier la fonction cube : dérivée, variations, représentation graphique.
Fonction cube. Dérivée de la fonction cube.
Utiliser les formules et les règles de dérivation pour déterminer la dérivée d’une fonction polynôme de degré inférieur ou égal à 3.
Dresser, à partir du signe de la dérivée, le tableau de variations d’une fonction polynôme de degré inférieur ou égal à 3.
Exploiter le tableau de variations d’une fonction polynôme ƒ de degré inférieur ou égal à 3 pour :
 - déterminer le nombre des solutions de l’équation ƒ(x) = c, où c est un nombre réel ;
 - déterminer les éventuels extremums locaux de la fonction ƒ.
Fonction polynôme de degré 3.
Exemples d’algorithmes ou d’activités numériques
- Déterminer un encadrement ou une valeur approchée par balayage d’une solution d’une équation du type ƒ(x) = g(x) lorsqu’on sait qu’elle existe dans un intervalle donné.
Commentaires :
 - Constater, à l’aide de la fonction cube, que le seul fait que la dérivée d’une fonction s’annule en un point ne suffit pas pour conclure que cette fonction possède un extremum local en ce point.
 - Lorsque la dérivée d’une fonction polynôme de degré 3 n’est pas facilement factorisable, l’outil numérique peut permettre de déterminer les racines éventuelles de la dérivée ; ceci permet d’établir le tableau de variations de cette fonction.

2.3 - Fonctions exponentielles et logarithme décimal
Représenter graphiquement les fonctions exponentielles de base q, définies sur un intervalle donné, par x ? q x (avec q nombre réel strictement positif et différent de 1).
Utiliser les propriétés opératoires des fonctions exponentielles étudiées pour transformer des écritures numériques ou littérales.
Fonctions exponentielles de base q, définies sur un intervalle donné par x ? q x (avec q nombre réel strictement positif et différent de 1).
Variations des fonctions exponentielles de base q, définies sur un intervalle donné par x ? q x (avec q nombre réel strictement positif et différent de 1).
Propriétés opératoires des fonctions exponentielles étudiées.
Représenter graphiquement la fonction logarithme décimal sur un intervalle donné.
Fonction logarithme décimal x ? log(x). Variations de la fonction logarithme décimal. Propriétés opératoires de la fonction logarithme décimal.
Résoudre par le calcul, graphiquement, ou à l’aide d’outils numériques des équations du type q x = a et log(x) = a ou des inéquations du type q x ? a (ou q x ? a) et log(x) ? a (ou log(x) ? a).
Résolution d’équations du type q x = a et log(x) = a ou d’inéquations du type q x ? a (ou q x ? a) et log(x) ? a (ou log(x) ? a).
Exemples d’algorithmes ou d’activités numériques
 - Déterminer un encadrement ou une valeur approchée par balayage d’une solution d’une équation du type ƒ(x) = g(x) lorsqu’on sait qu’elle existe dans un intervalle donné.
Commentaires
 - Les fonctions exponentielles sont à présenter sur l’ensemble des réels positifs comme prolongement, à des valeurs positives non entières, des suites géométriques de premier terme 1 et de raison q strictement positive. La fonction obtenue sur ?+ est étendue à l’ensemble des réels en posant q -x=1 / q x et ses variations sont admises.
 - En s’appuyant sur les propriétés des suites géométriques de raison strictement positive, différente de 1, les propriétés opératoires des fonctions x ? q x et leurs variations sont admises après conjecture à l’aide d’outils numériques.
 - La fonction logarithme décimal est introduite à partir de la fonction ƒ définie par ƒ(x) = 10 x et de son tableau de variations : le logarithme décimal de b, pour b strictement positif, est défini comme l’unique solution de l’équation 10 x = b.
 -  L’identité log(10 x ) = x se déduit de la définition.
 - Selon les besoins, on pourra présenter et utiliser du papier semi-logarithmique, notamment pour exploiter le tracé d’une droite sur ce type de support papier.

3.1 Calculs commerciaux et financiers
(pour les spécialités de baccalauréat professionnel ne comportant pas d’enseignement de physique-chimie)
Calculer le montant du capital obtenu après n périodes d’un placement à intérêts composés.
Déterminer la durée n de placement d’un capital initial C0 à un taux t donné, pour obtenir un capital donné.
Intérêts composés. Formule Cn = C0 (1 + t ) n.
Compléter un tableau d’amortissement.
Emprunt : remboursement par annuités constantes, remboursement par amortissement constant. Coût d’un emprunt.
Calculer un taux mensuel équivalent à un taux annuel donné.
Calculer un taux moyen.
Taux mensuel, taux annuel, taux moyen.
Exemples d’algorithmes et d’activités numériques
 - Calculer le capital obtenu après

3.1 - Vecteurs (groupement B)
Déterminer graphiquement les coordonnées d’un vecteur dans l’espace muni d’un repère orthonormé.
Représenter, dans l’espace muni d’un repère orthonormé, un vecteur dont les coordonnées sont données.
Dans l’espace muni d’un repère orthonormé :
- coordonnées cartésiennes d’un point ;
- coordonnées d’un vecteur.
Calculer la norme d’un vecteur dans l’espace muni d’un repère orthonormé.
Norme d’un vecteur dans l’espace muni d’un repère orthonormé.
Calculer les coordonnées du vecteur somme de deux vecteurs dans l’espace muni d’un repère orthonormé.
Coordonnées du vecteur somme de deux vecteurs donnés dans l’espace muni d’un repère orthonormé.
Reconnaître, à l’aide de leurs coordonnées, des vecteurs égaux ou colinéaires dans l’espace muni d’un repère orthonormé.
Coordonnées du produit d’un vecteur par un nombre réel dans l’espace muni d’un
Commentaires :
- Le lien entre le produit d’un vecteur par un réel et la colinéarité est établi.
- La norme d’un vecteur est définie comme la longueur d’un de ses représentants.

3.2 - Trigonométrie (groupement A)
Établir des liens entre le vecteur de Fresnel d’une tension ou d’une intensité sinusoïdale de la forme a.sin(ω t +φ) et la courbe représentative de la fonction qui à t associe a.sin(ω t +φ).
Représentation de Fresnel d’une grandeur sinusoïdale.
Résoudre les équations de la forme :
cos(x) = a, sin(x) = b sur l’intervalle ]-π,π] et sin(ω t +φ) = c sur un intervalle approprié au contexte.
Équations de la forme cos x = a, sin x = b et sin(ω t +φ) = c sur un intervalle donné.
Commentaires :
- Ce module est traité en s’appuyant sur des exemples concrets issus du domaine professionnel.

Algorithmique et programmation
(groupements A, B et C)
Ce module permet aux élèves de consolider et d’approfondir l’étude de l’algorithmique et de la programmation commencée dans les classes antérieures.

Liens avec la première professionnelle.
En classe de première, les élèves ont travaillé sur les notions de variable, d’instruction conditionnelle et de boucle ainsi que sur l’utilisation des fonctions et ont découvert les listes. En classe terminale, ils approfondissent ces différentes notions.
En continuité avec les classes de seconde et de première, le langage utilisé est le langage Python.
Analyser un problème.
Décomposer un problème en sous-problèmes.
Repérer les enchaînements logiques et les traduire en instructions conditionnelles et en boucles.
Séquences d’instructions, instructions conditionnelles, boucles bornées (for) et non bornées (while).
Choisir ou reconnaître le type d’une variable.
Réaliser un calcul à l’aide d’une ou de plusieurs variables.
Types de variables : entiers, flottants, chaînes de caractères, booléens. Affectation d’une variable.
Modifier ou compléter un algorithme ou un programme.
Concevoir un algorithme ou un programme simple pour résoudre un problème.
Comprendre et utiliser des fonctions.
Compléter la définition d’une fonction.
Structurer un programme en ayant recours à des fonctions pour résoudre un problème donné.
Arguments d’une fonction. Valeur(s) renvoyée(s) par une fonction.
Générer une liste.
Manipuler des éléments d’une liste (ajouter, supprimer, extraire, etc.).
Parcourir une liste.
Itérer une ou plusieurs instructions sur les éléments d’une liste.
Liste
Commentaires :
- Les notions abordées dans ce module ne font pas l’objet d’un cours spécifique et sont travaillées en situation.
- La maîtrise des propriétés des différents types de variables n’est pas attendue.
- Pour les fonctions en Python, dans des cas simples, on ne donne pas systématiquement aux élèves l’en-tête de la fonction (nom et arguments).
- Les notions relatives aux types de variables et à l’affectation sont consolidées. Pour un algorithme écrit en langage naturel, on utilise le symbole ← pour désigner l’affectation, alors qu’en langage Python, on utilise le signe =.
- L’accent est mis sur la programmation modulaire qui permet de découper une tâche complexe en tâches plus simples.
- Les listes peuvent être générées en extension, par ajouts successifs d’éléments, et en compréhension.
- La génération de listes en compréhension et en extension est mise en lien avec la notion d’ensemble. Les conditions apparaissant dans les listes définies en compréhension permettent de travailler la logique.
- Afin d’éviter toute confusion, il est recommandé de se limiter aux listes sans présenter d’autres types de collections.

Automatismes
(groupements A, B et C)
Liste non exhaustive d’automatismes à travailler
Les automatismes figurant dans les programmes de seconde et de première professionnelles continuent à être entretenus.
1.1 - Statistiques à 2 variables
-
1.2 - Probabilités
Calcul de la probabilité : d’un événement, de l’événement contraire ? connaissant celle de l’événement A.
Calcul de la probabilité de la réunion d’événements incompatibles.
Calcul de la probabilité de la réunion de deux événements.
Calcul de la probabilité de l’intersection de deux événements.
Exploitation de représentations de données : tableaux croisés d’effectifs, diagrammes.
Calcul de probabilités conditionnelles.
2.1 - Suites numériques 2
Calcul du terme de rang donné d’une suite arithmétique dont le premier terme et la raison sont donnés.
2.2 - Fonctions polynômes de degré 3
Visualisation, à partir de la représentation graphique donnée d’une fonction polynôme ƒ de degré 2, du nombre possible de solution(s) de l’équation ƒ(x) = 0.
Écriture de la forme factorisée d’un polynôme de degré 2 dont les racines et le coefficient dominant sont connus.
Utilisation des formules et des règles de dérivation pour déterminer la dérivée d’une fonction polynôme de degré inférieur ou égal à 2.
3.2 - Trigonométrie
(groupement A)
-
3.1 - Vecteurs
(groupement B)
Construction d’un vecteur du plan2 obtenu comme :
- somme de deux vecteurs ;
- produit d’un vecteur par un nombre réel non nul.
Commentaires :
- Ce module est traité en s’appuyant sur des exemples concrets issus du domaine professionnel.

2 Cet automatisme n’est à tester que dans les classes préparant à un baccalauréat du groupement A ou du groupement B.

Vocabulaire ensembliste et logique
(groupements A, B et C)
Connaître les notions d’élément d’un ensemble, de sous-ensemble, d’appartenance et d’inclusion, de réunion, d’intersection et de complémentaire et savoir utiliser les symboles de base correspondant : ∈, ⊂, ?, ?, ainsi que la notation des ensembles de nombres et des intervalles du type [ a ; b ] , ] a ; b [ , [ a ; b [ , ] a ; b ] avec a et b réels.
Ils rencontrent également la notion de couple.
Pour le complémentaire d’un sous-ensemble A de E, on utilise la notation des probabilités ?.
Pour ce qui concerne le raisonnement logique, les élèves rencontrent à la faveur d’exemples :
 - Les connecteurs logiques « et », « ou » ;
 - le quantificateur « quel que soit » et le quantificateur « il existe » (les symboles ∀ et ∃ sont hors programme) ;
 - des implications et équivalences logiques ;
 - la réciproque d’une implication ;
 - l’utilisation d’un contre-exemple pour infirmer une proposition universelle ;
 - des raisonnements par disjonction des cas, des raisonnements par l’absurde.
Les élèves distinguent les utilisations possibles du symbole = (égalité, identité, équation) et le statut des lettres utilisées (variable, indéterminée, inconnue, paramètre).
Baccalauréat TERMINALE
BOEN 2019 applicable septembre 2021
Programme complémentaire
en vue de la préparation à une poursuite d’études

Objectifs :
Le programme complémentaire de mathématiques est destiné à apporter des renforts notionnels aux élèves dans le cadre de l’accompagnement au choix d’orientation, en fonction de la poursuite d’études envisagée.

Les modules du programme complémentaire à traiter seront déterminés en fonction du projet d’orientation de l’élève.

Calcul intégral
Déterminer les primitives des fonctions usuelles par lecture inverse d’un tableau des dérivées.
Déterminer, avec ou sans outils numériques, les primitives d’une somme de fonctions, du produit d’une fonction par un réel.
Primitives d’une fonction sur un intervalle.
La fonction F étant une primitive d’une fonction ƒ sur un intervalle, F + k (où k est une constante) est aussi une primitive de ƒ.
Primitives d’une somme de fonctions, du produit d’une fonction par un réel.
Calculer l’intégrale, sur un intervalle [ a , b ], d’une fonction ƒ admettant une primitive F, avec ou sans outils numériques.
Interpréter l’intégrale d’une fonction définie et positive sur un intervalle [ a , b ] comme une aire.
Définition de l’intégrale, sur un intervalle [ a , b ], d’une fonction ƒ admettant une primitive F sur cet intervalle : ∫ƒ(x)dx=F(b)-F(a)
Commentaires :
 - Il n’est imposé aucune virtuosité calculatoire.
 - Le calcul d’aire est plus spécifiquement destiné aux élèves choisissant une poursuite d’études dans le secteur industriel.
 - Une approximation de la valeur de l’intégrale d’une fonction positive sur un intervalle [ a , b ] par la méthode des rectangles peut être obtenue à l’aide des outils numériques.

Fonctions logarithme népérien et exponentielle
Étudier les variations et représenter graphiquement la fonction logarithme népérien, sur un intervalle donné.
Utiliser les propriétés opératoires de la fonction logarithme népérien pour transformer des écritures numériques ou littérales.
Fonction logarithme népérien x ? ln(x). Définition du nombre e. Propriétés opératoires de la fonction logarithme népérien.
Passer de ln(x) = a  à  x = e a et inversement, a étant un réel et x un réel strictement positif.
Utiliser les propriétés opératoires de la fonction exponentielle pour transformer des écritures numériques ou littérales.
Étudier les variations et représenter graphiquement la fonction exponentielle sur ?.Fonction exponentielle de base e.
Propriétés opératoires de la fonction exponentielle de base e.
Commentaires :
 -  La fonction logarithme népérien x ? ln(x) est la fonction définie sur l’ensemble des réels strictement positifs, qui s’annule en 1 et dont la dérivée est la fonction inverse.
 - On pourra faire le lien entre la fonction logarithme népérien et la fonction logarithme décimal.
 - Les propriétés opératoires de la fonction logarithme népérien sont admises.
 - Le nombre e étant défini comme l’unique solution de l’équation ln(x) = 1, la représentation graphique de la fonction x ? e x est obtenue, à l’aide des outils numériques, à partir de celle de la fonction logarithme népérien.
 - On fera remarquer que la fonction exponentielle introduite dans ce module est un cas particulier des fonctions x ? q x.

Nombres complexes
Calculer et interpréter géométriquement dans le plan rapporté à un repère orthonormé direct, la partie réelle, la partie imaginaire, le conjugué, le module d’un nombre complexe et un argument d’un nombre complexe non nul.
Passer de la forme algébrique à la forme trigonométrique et réciproquement.
Forme algébrique :
- partie réelle, partie imaginaire, conjugué, module ;
- égalité de deux nombres complexes ;
- représentation dans le plan rapporté à un repère orthonormé direct, affixe d’un point, d’un vecteur ;
- somme, produit, quotient de deux nombres complexes ;
- conjugué d’une somme, d’un produit, d’un quotient ;
- module d’un produit et d’un quotient.
Argument et forme trigonométrique d’un nombre complexe non nul.
Commentaires :
 - L’image de la somme et celle du produit de deux nombres complexes peuvent être illustrées à l’aide d’un logiciel de géométrie dynamique.

Produit scalaire de deux vecteurs
du plan rapporté à un repère orthonormé
Utiliser les trois expressions du produit scalaire de deux vecteurs pour déterminer des longueurs et des angles.
Définition du produit scalaire de deux vecteurs du plan rapporté à un repère orthonormé.
Propriétés du produit scalaire de deux vecteurs :
u? ⋅ v?  =  v? ⋅  u?  
α ( u? ⋅ v?  ) = (α u? ) ⋅ v? 
u? ⋅ ( v? + w?? ) = u? ⋅ v? + u? ⋅ w
Reconnaître des vecteurs orthogonaux, à l’aide de leurs coordonnées dans un repère orthonormé.
Vecteurs orthogonaux : deux vecteurs u? et v? sont orthogonaux si et seulement si leur produit scalaire est nul.
Commentaires :
 - Le produit scalaire de deux vecteurs du plan rapporté à un repère orthonormé est défini par l’une des trois expressions suivantes ; les deux autres sont admises :
     u? ⋅ v? =1/2 ( ?u? + v? ?2 -  ?u? ?2 -  ?v? ?2 ) ;
 - Si u? ou v? est nul alors u? ⋅ v? = 0. Si u? et v? sont tous les deux différents du vecteur nul alors u? ⋅ v? = ?u? ? × ?v? ? × cos(θ)  avec θ = (u? ,v? ).
   La notion d’angle orienté de vecteurs est abordée de façon intuitive.
 - Si les vecteurs u? et v? ont pour coordonnées respectives (x , y ) et ( x’, y’ ) alors u? ⋅ v? = xx’ + yy’